Молитвы абитуриентов, составляющих ВНО/НМТ по математике, были услышаны и в тестовую тетрадь с 2021 года кроме блока задач начали добавлять блок с формулами, которые можно использовать во время экзамена. Это значительно облегчило подготовку к мультипредметному тесту, поскольку школьникам больше не нужно наизусть учить все формулы. Однако своеобразная шпаргалка поможет не всем. Мало видеть ее перед глазами – нужно ее понимать. В этом материале мы собрали все формулы, которые будут на НМТ по математике в 2024 году, а также добавили примеры задач с объяснением, как использовать эти формулы.
Формулы, которые будут на ЗНО/НМТ
Таблица формул для НМТ по математике разделена на две части – алгебра и геометрия. Всего шпаргалка состоит из трех листов формата А4 и выглядит так. Разберем обе части с формулами по темам.
Формулы из алгебры
Таблица квадратов от 10 до 49
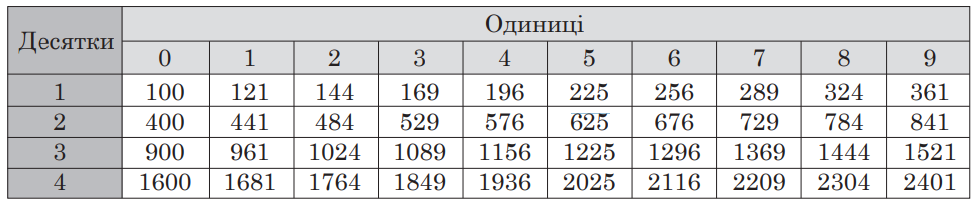
Это таблица, содержащая квадраты чисел от 10 до 49. Квадрат числа – это результат умножения числа на себя. Такая таблица помогает легко найти квадраты чисел в указанном диапазоне без необходимости их расчета вручную.
Например, вам нужно узнать квадрат числа 36. Для этого в столбце с десятками выбираем 3, а в столбце с единицами выбираем 6. В строке, где они соединяются, будет значение квадрата (1296).
Читайте также: Как понять математику: советы для взрослых и детей
Таблица сокращенного умножения
Формулы сокращенного умножения – это математические формулы, помогающие упрощать выражения или разлагать их на произведения биномов (выражений с двумя членами). Они полезны для алгебраических расчетов, преобразований, упрощения сложных выражений и уравнений.

На НМТ может случиться задача, при которой нужно упростить уравнение, используя формулы сокращенного умножения. К примеру:
(x + 3)² – (x – 2)²
Решение:
- Разлагаем первое слагаемое (x + 3)², используя формулу (a + b)² = a² + 2ab + b². Получаем: x²+6x+9.
- Разлагаем второе слагаемое (x – 2)² по формуле (a – b)² = a² – 2ab + b². Получаем: x² – 4x+4.
- Теперь вычтем второе слагаемое из первого: (x² + 6x + 9) – (x² – 4x + 4) = x² + 6x + 9 – x² + 4x – 4.
- Проведем упрощение: 10x+5
Следовательно, упрощенное выражение для (x + 3)² – (x – 2)² равно 10x + 5.
Квадратное уравнение
Квадратное уравнение – это уравнение, в котором переменная приподнята к квадрату и содержит коэффициенты. Обычно квадратное уравнение выглядит так:
ax² + bx + c = 0, где:
- x – неизвестная переменная, которую мы пытаемся найти;
- a, b и c – коэффициенты, где a не равно 0 (иначе это не будет квадратным уравнением).
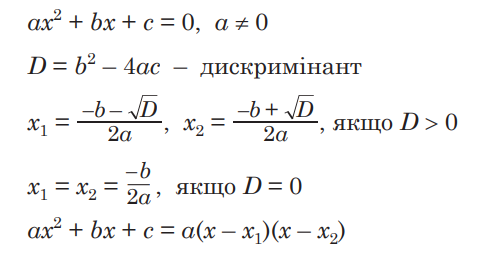
Табличка степеней
Степень – это числовой показатель, указывающий, сколько раз определенное число (основа) возвышается до степени. В математических выражениях степень обозначается как верхний индекс справа от основания. Например, в выражении a⁵, цифра 5 – это степень, a – это основание. Это означает, что a возносится к степени 5, то есть умножается сама на себя 5 раз.
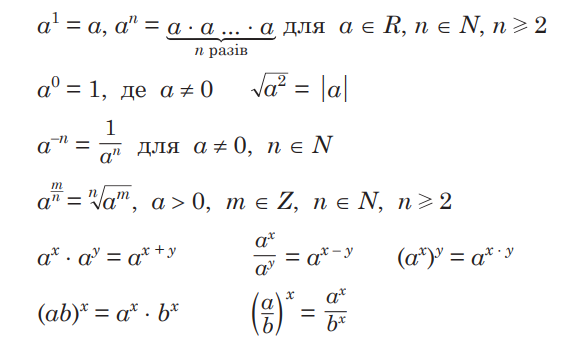
Логарифмы
Логарифмы – это математическая функция, которая используется для определения степени, к которой нужно преподнести определенное число (основу логарифма), чтобы получить другое число. Например, log₁₀(1000) = 3, поскольку 10 в третьей степени равно 1000.
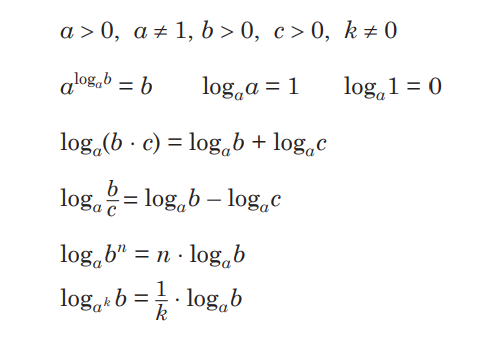
Формулы арифметической и геометрической прогрессий
Арифметическая прогрессия – это последовательность чисел, где каждое последующее число образуется сложением одного и того же числа (разницы) к предыдущему. Эта разница называется разницей арифметической прогрессии и обозначается как d.
Геометрическая прогрессия – это последовательность чисел, где каждое последующее число образуется умножением предыдущего на фиксированный множитель, называемый знаменателем геометрической прогрессии. Знаменатель геометрической прогрессии обозначается как q .
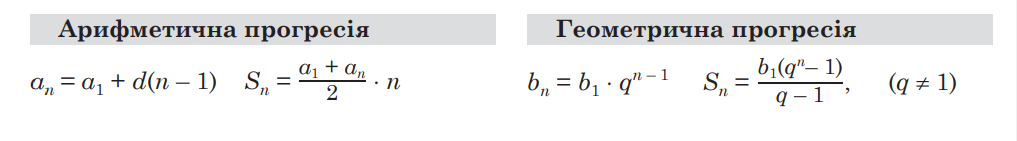
Если вы не можете похвастаться отличными знаниями по математике, однако планируете сдавать НМТ в 2024 году, стоит записаться на дополнительные занятия с репетитором по математике в БукиСкул. Индивидуальный подход и правильная программа занятий, настроенная на ваши потребности – именно то, что нужно для качественной подготовки к НМТ.
Производная функции
Производная функции – это способ измерения, показывающий, насколько быстро меняется функция при незначительных изменениях аргумента. Другими словами, она указывает, как стремительно либо медлительно изменяется функция в каждой конкретной точке. К примеру, если мы имеем функцию, которая представляет скорость автомобиля, то ее производная покажет нам, насколько быстро меняется скорость автомобиля в определенный момент времени.
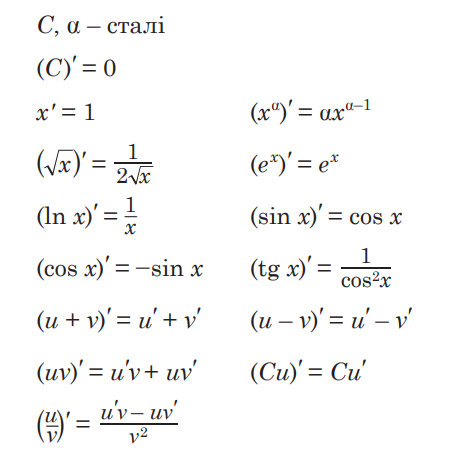
Читайте также: Интересные математические загадки и задачи
Формулы по геометрии
Тригонометрия
Главные тригонометрические формулы связаны с тремя функциями: синус, косинус и тангенс. Синус угла в прямоугольном треугольнике определяется отношением противоположной стороны к гипотенузе, косинус – отношением прилегающей стороны к гипотенузе, тангенс – отношением противоположной стороны к близлежащей. Их находят по следующим формулам:
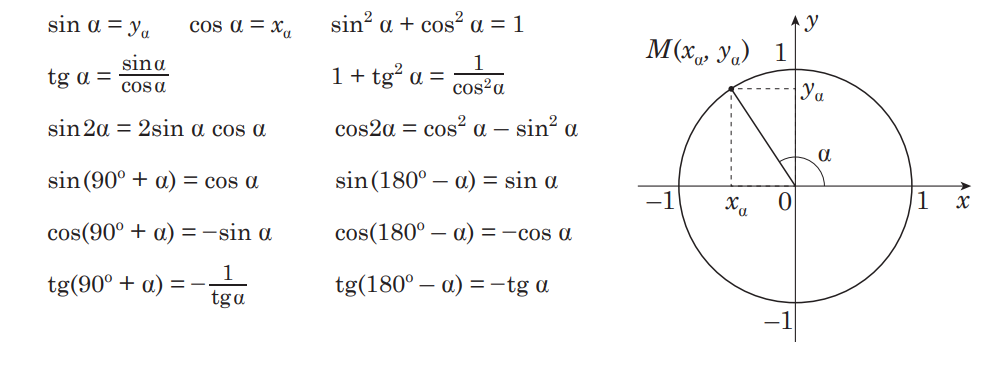
Ниже приведена таблица значений тригонометрических функций некоторых углов:

Формулы для треугольников
- Произвольный треугольник – это любой треугольник, который не является равносторонним или равнобедренным.
- Прямоугольный треугольник – это треугольник, у которого один из углов прямой, то есть равен 90 градусов. В прямоугольном треугольнике есть 2 катета (более короткие стороны) и гипотенуза (более длинная сторона).
В справочных материалах по математике есть формулы для определения периметра и площади, а также теорема Пифагора, которую используют для определения сторон в прямоугольном треугольнике.

Формулы для четырехугольников
Основные свойства четырехугольников:
- Параллелограмм:
- В параллелограмме все противоположные стороны параллельны (имеют одинаковый наклон).
- Противоположные углы параллелограмма равны.
- Сумма углов параллелограмма равна 360 градусам.
- Диагонали параллелограмма пересекаются посередине.
- Прямоугольник:
- У прямоугольника все углы равны 90 градусам, то есть он имеет четыре прямых угла.
- Противоположные стороны прямоугольника параллельны.
- Диагонали прямоугольника равны по длине и пересекаются посередине под прямым углом.
- Ромб:
- У ромба все стороны имеют одинаковую длину.
- Противоположные углы ромба равны.
- Диагонали ромба перпендикулярны друг другу и пересекаются в середине ромба.
- Трапеция:
- Трапеция имеет одну пару параллельных сторон и одну пару непараллельных сторон.
- Углы трапеции не обязательно равны.
- Верхняя и нижняя стороны трапеции могут иметь разную длину.
Формулы окружности и круга
Окружность – это множество всех точек, расположенных на одинаковом расстоянии от центральной точки, называемой центром окружности. Круг – это плоскость, ограниченная окружностью (внешним «контуром») круга.
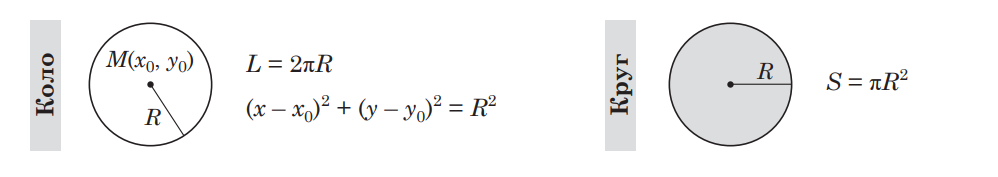
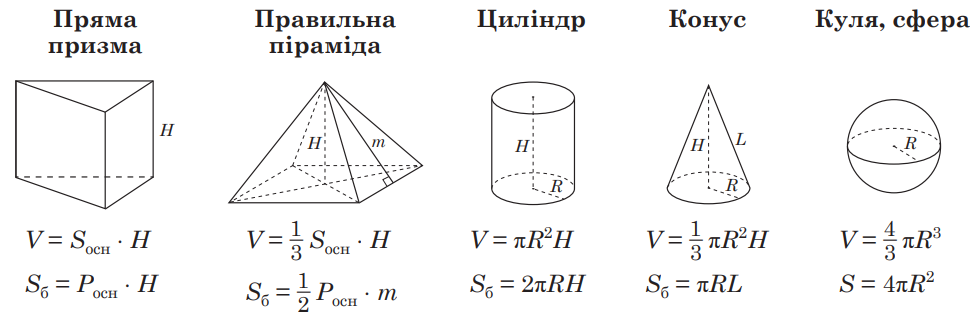
Формулы объемных фигур и тел
Здесь приведены формулы определения площади и объема таких объемных фигур: прямая призма, правильная пирамида, цилиндр, конус, шар (сфера).
Координаты и векторы
Вектором называется направленный отрезок. Координаты вектора представляют собой координаты конечной точки этого вектора, если вектор расположен так, что его начало располагается в начале координат.
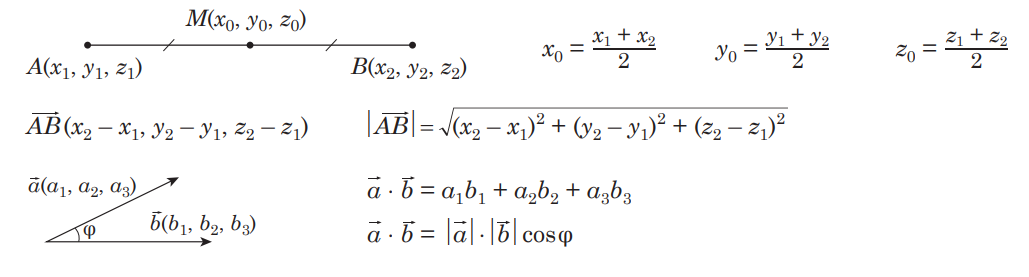
Отлично составленное НМТ – это залог поступления на бюджет в топовые университеты Украины. Если вам нужна помощь в подготовке к тестированию, запишитесь на индивидуальные уроки с репетиторами в школе БукиСкул. У нас есть репетиторы по математике, украинскому, английскому, истории Украины и другим предметам школьной программы.